Trees

Trees are a kind of non-linear data structure that is used to store data in a hierarchical manner.

Some of the basic terminologies that would be common for alls kinds of trees:

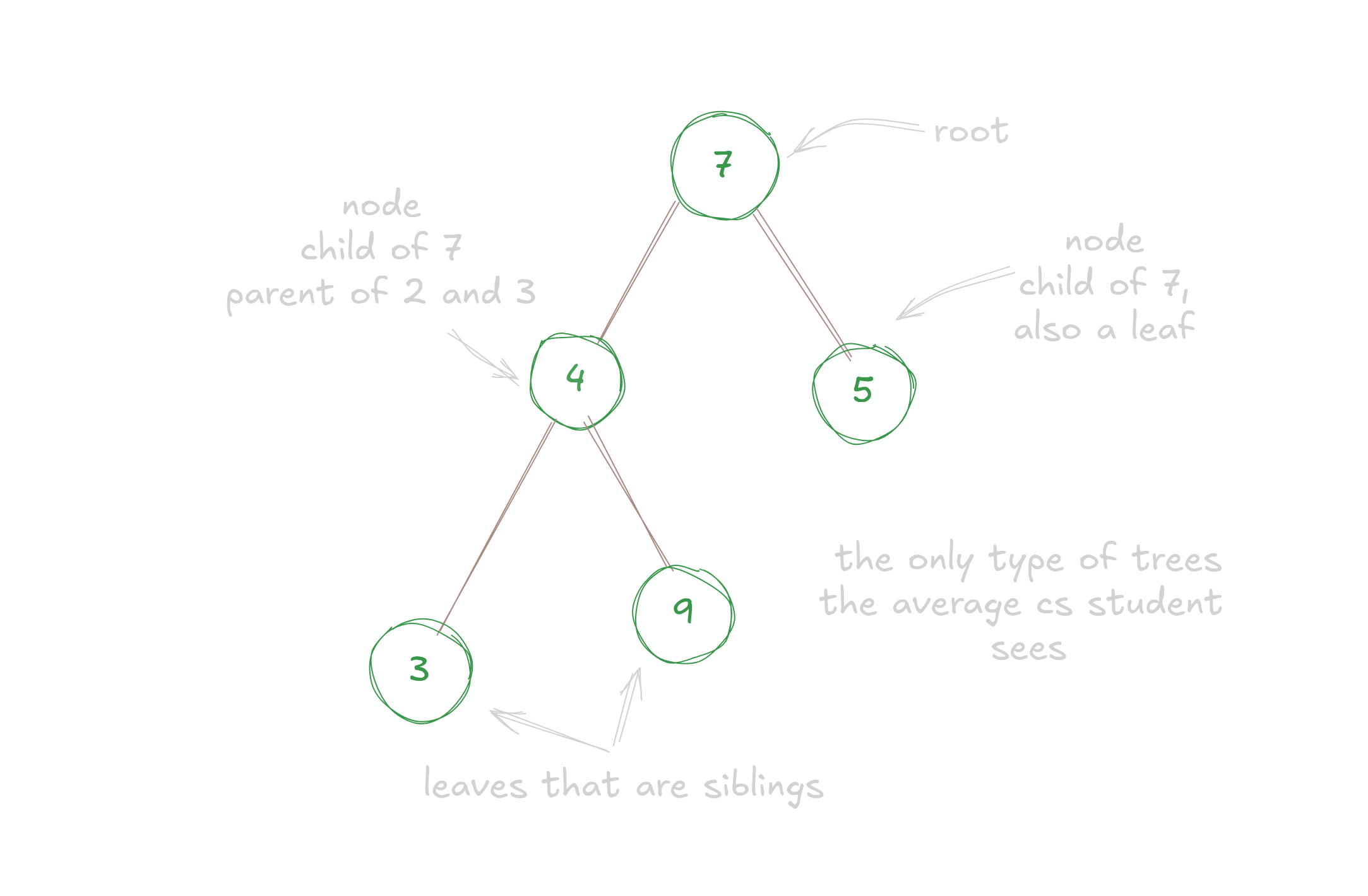
1. Root: The topmost node in a tree. In the above example, it is 7.
2. Parent: A node that has children. In the above example, 4 is the parent of of 3 and 9. Each Root is a parent but not all parents are roots.
3. Child: A node that has a parent. In the above example, 3 and 9 are children of 4.
4. Leaf / External Node: A node that has no children. In the above example, 3, 5 and 9 are leaves.
5. Siblings: Nodes that share the same parent. In the above example, 3 and 9 are siblings.
6. Internal Node: A single element in a tree that has atleast 1 child. In the above example, 4 is a node.
7. Depth Of A Node: Can be defined as the number of branches between the node and the root.
8. Height Of A Tree: Can be defined as the number of branches between the node and the deepest leaf.
9. Ancestor: A node that lies on the path between the root and the node. In the above example, 4 is an ancestor of 3.
10. Descendant: A node that lies on the path between the node and the leaf. In the above example, 3 is a descendant of 4.
11. Degree Of A Node: The number of children a node has.
12. Degree Of A Tree: The maximum degree of a node in the tree among all the other nodes.

If a tree has n nodes, it will have n-1 edges.

Binary Trees

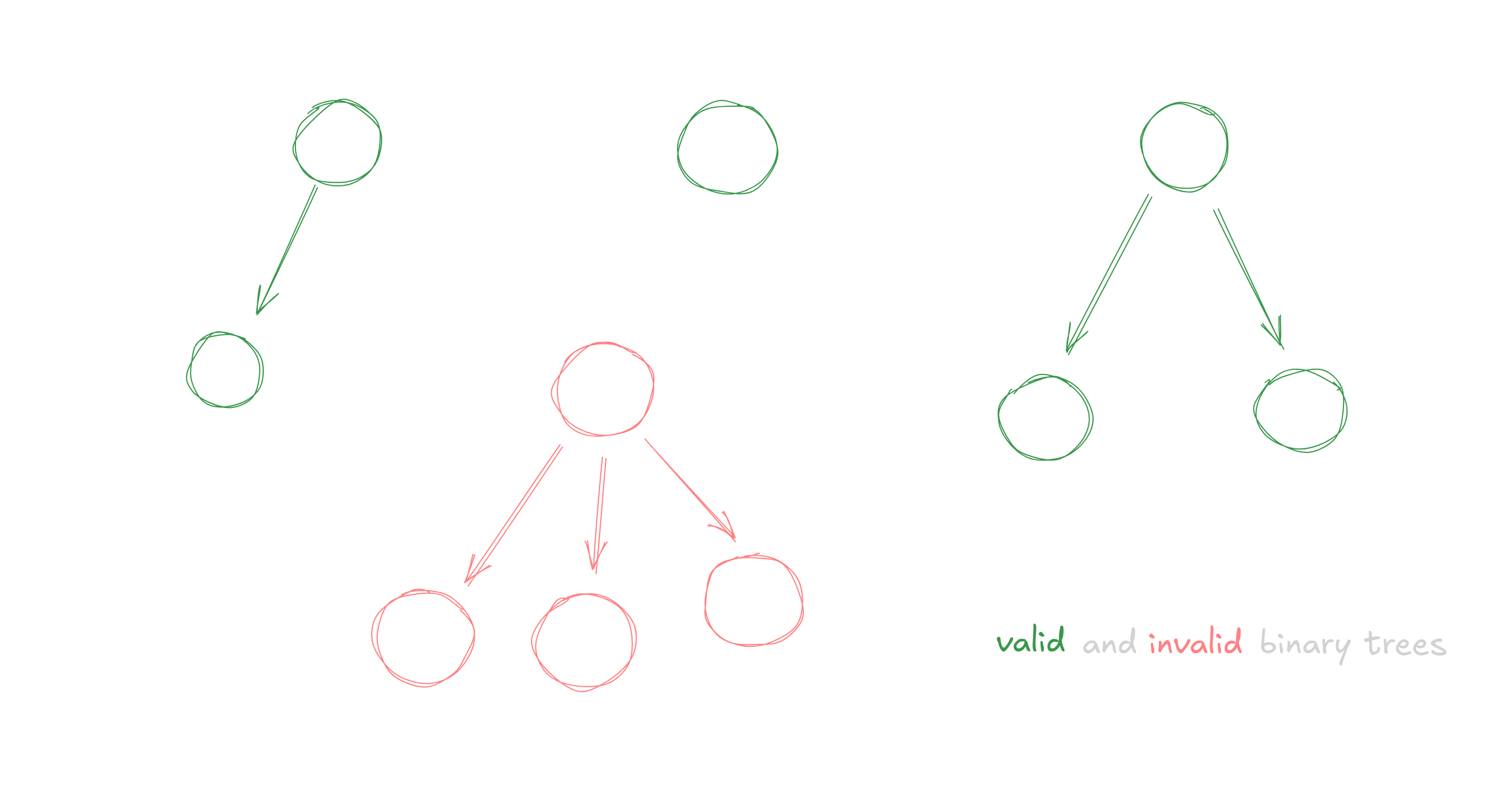
Binary is a type of tree in which each node has atmost 2 children i.e it has a degree of 2. The children are referred to as the left child and the right child.

The left child is always smaller than the parent and the right child is always greater than the parent.

Types Of Binary Trees

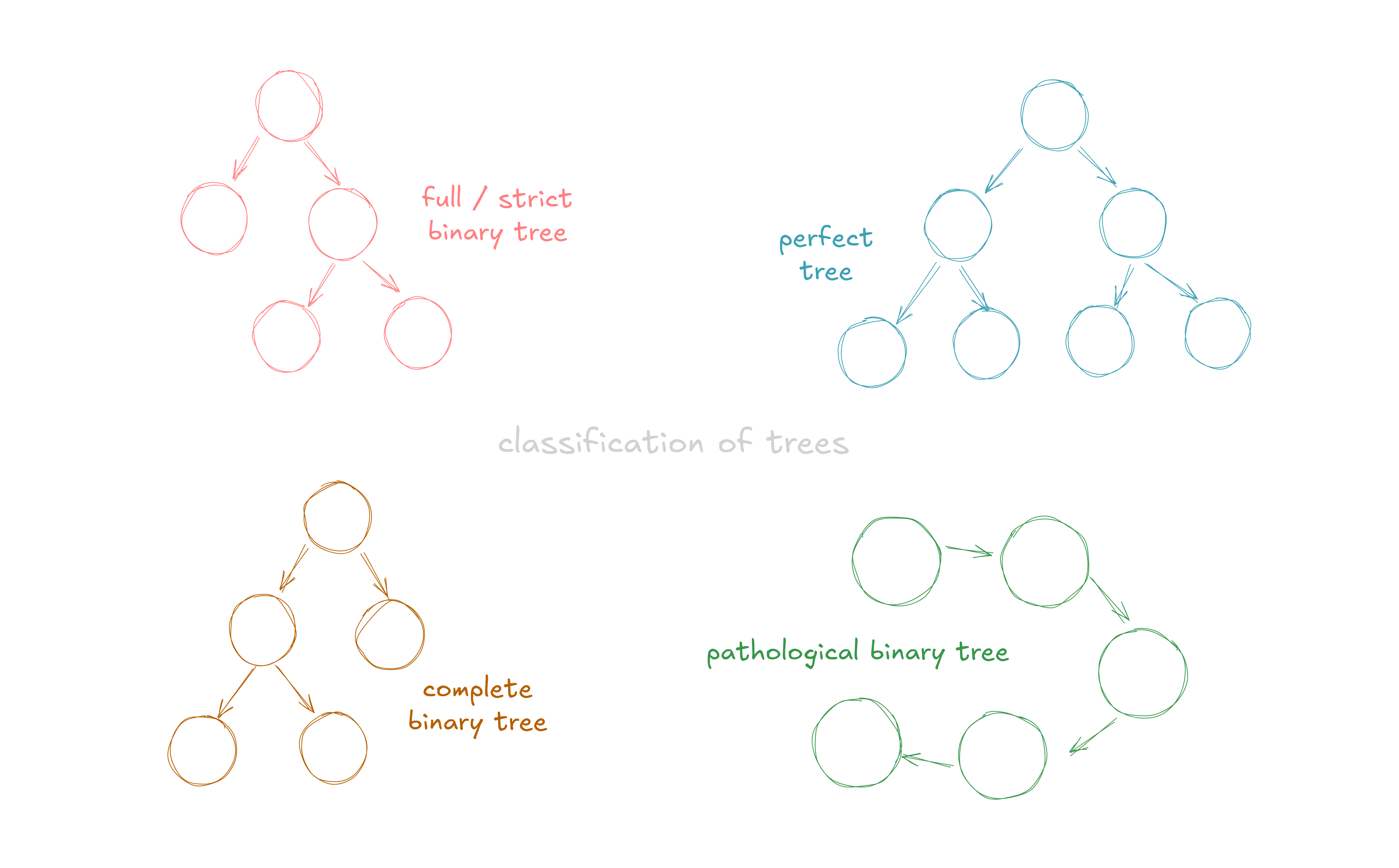
1. Full / Strict Binary Tree: A binary tree in which each node has either 0 or 2 children.

2. Perfect Binary Tree: A binary tree in which all the internal nodes have a degree of 2 and all the leaves are at the same level.

3. Complete Binary Tree: A binary tree in which all the levels are completely filled except for the last level. The last level is filled from left to right.

4. Degenerate / Pathological Tree: A tree in which each parent has only one child. It is basically a linked list.

5. Skewed Binary Tree: A tree in which all the nodes have only one child in one specific direction. It is a special case of a degenerate tree.

Representation Of Binary Trees

The first and the worse way of representing a binary tree is by using arrays. The array is filled from left to right starting from the root. If a node does not have a child, then we will a NULL in its place.

Let us take an example

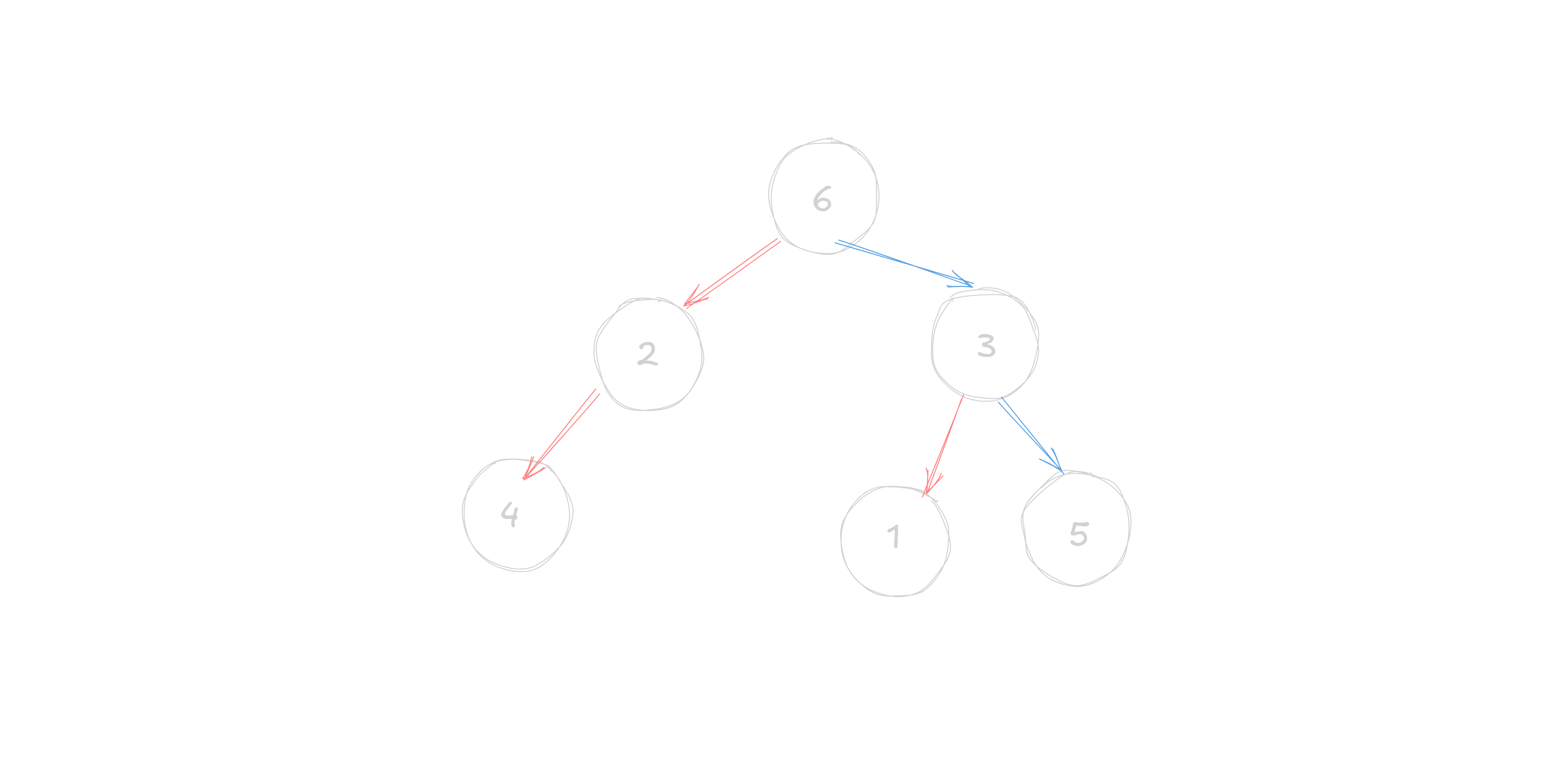
The array representation of the above tree would be:

[6, 2, 3, 4, NULL, 1, 9]

But this practice is almost never used because it is very inefficient. The second way of representing a binary tree is by using linked lists.

Linked Representation

Let us take the same example as above. Now we will express each node as a structure with 3 things, the value, the address of the left node and the address of the right node.

// If you already know some DSA
// you might find this similar to a doubly linked list.
struct Node {
    int data;
    struct Node* left;
    struct Node* right;
};

The linked representation of the above tree wouuld look like

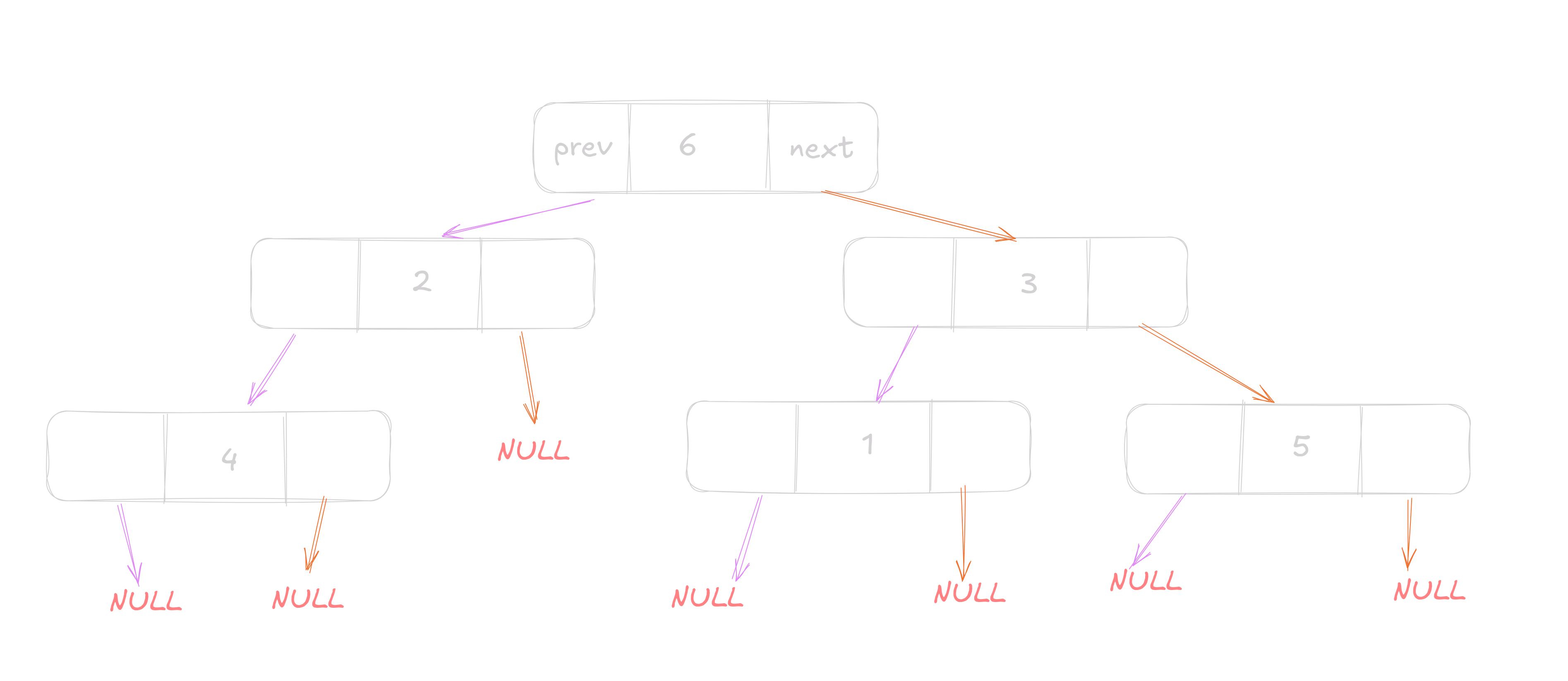
So let us define a very basic binary tree in C.

struct Node *root;
root = (struct Node*)malloc(sizeof(struct Node)); // Allocating memory for the root node
root->data = 6;
root->left = NULL;
root->right = NULL;

Here we have the most basic of a binary tree which has only 1 node (the root). If you did not understand what I did in the second line, please refer to my post on Dynamic Memory Allocation.

Now let us add some more nodes to extend this root

struct Node *p1, *p2;
p1 = (struct Node*)malloc(sizeof(struct Node));
p2 = (struct Node*)malloc(sizeof(struct Node));
 
p1->data = 2;
p1->left = NULL;
p1->right = NULL;
 
p2->data = 3;
p2->left = NULL;
p2->right = NULL;

Now we can attach these newly created nodes to the root

root->left = p1;
root->right = p2;

Traversing A Binary Tree

There are mainly three ways to traverse a binary tree, Preorder, Inorder and Postorder. Preorder visits the root first, then left and right subtrees. Inorder visits the left subtree, then the root, and finally the right subtree. Postorder visits left and right subtrees before the root.

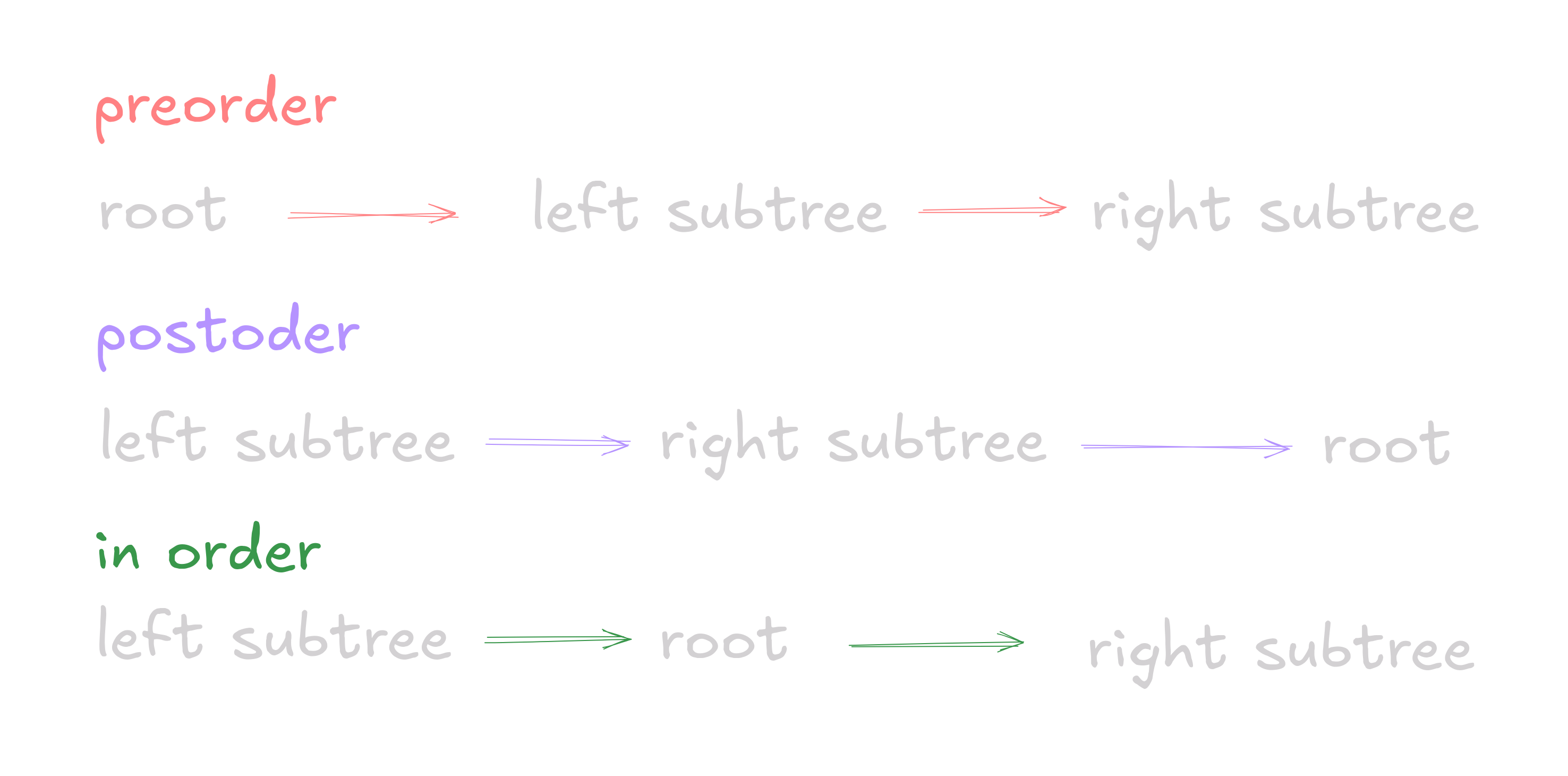
Taking the same example as above we would get

Preorder: 6, 2, 4, 3, 1, 5

1. Start at the root (6)
2. Visit the left subtree (2, 4)
3. Visit the right subtree (3, 1, 5)

Inorder: 4, 2, 6, 1, 3, 5

1. Visit the left subtree (4, 2)
2. Visit the root (6)
3. Visit the right subtree (1, 3, 5)

Postorder: 4, 2, 1, 5, 3, 6

1. Visit the left subtree (4, 2)
2. Visit the right subtree (1, 5, 3)
3. End at the root (6)

C code for preorder traversal would be:

void traverse_preorder(struct node*root) {
    if (root != NULL) {
        printf("%d ", root->data);
        traverse_preorder(root->left);
        traverse_preorder(root->right);
    }
}

C code for postorder traversal would be:

void traverse_postorder(struct node*root) {
    if (root != NULL) {
        traverse_postorder(root->left);
        traverse_postorder(root->right);
        printf("%d ", root->data);
    }
}

And lastly, the C code for inorder traversal would be:

void traverse_inorder(struct node*root) {
    if (root != NULL) {
        traverse_inorder(root->left);
        printf("%d ", root->data);
        traverse_inorder(root->right);
    }
}

Finding the height of a binary tree.

Height of the binary tree is the longest path between the root node and a leaf node.

int height(struct Node* root) {
  // base case: 
  if (root == NULL) {
    return 0;
  }
 
  int left = height(root->left);
  int right = height(root->right);
 
  if (left > right) {
    return left + 1;
  } else {
    return right + 1;
  }
}

Let us again take our example binary tree

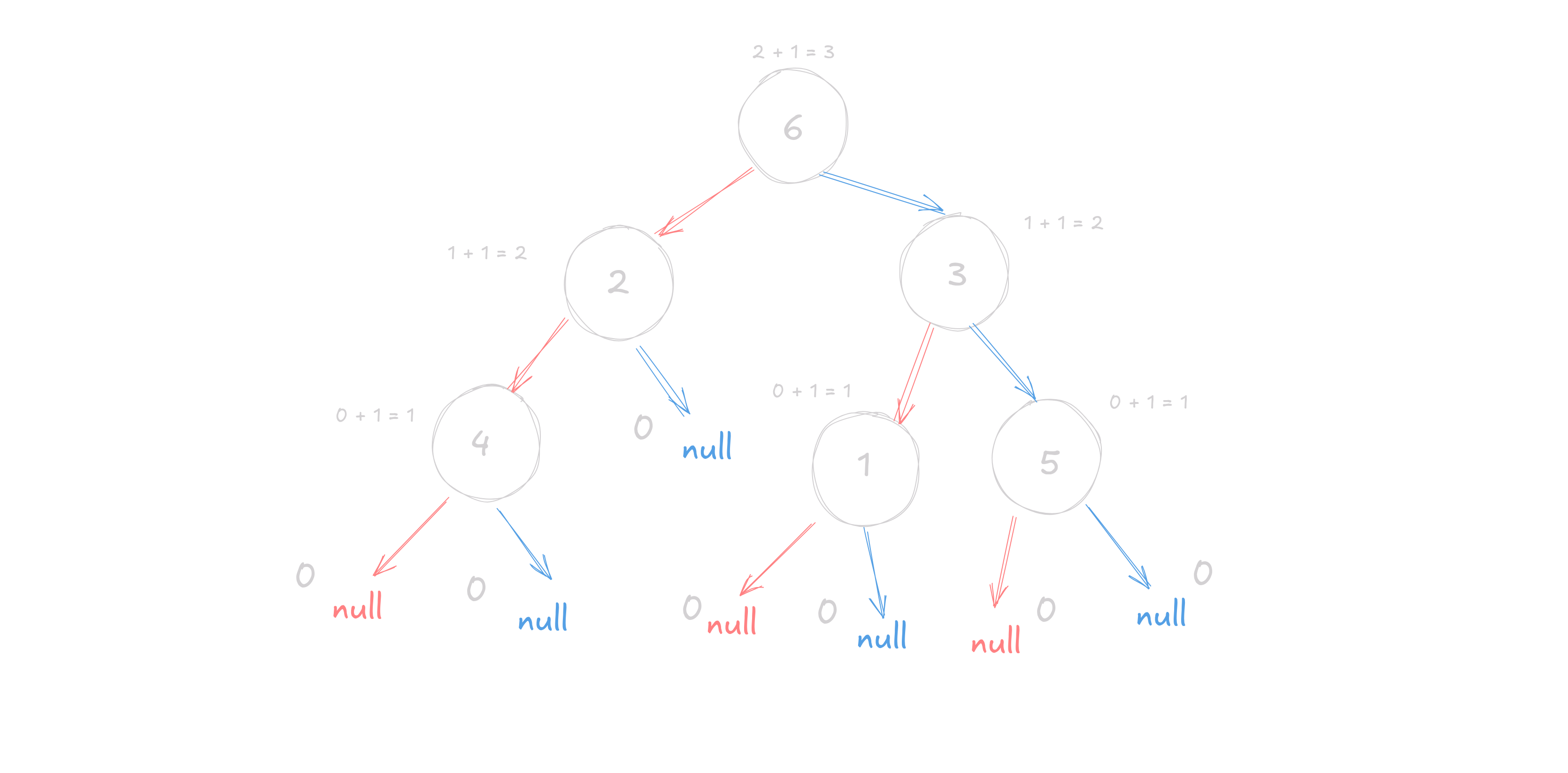
So starting from the root node 6, it is clearly not, null, so it goes to 2 and 3. Now taking 2 individually, as 2 is obviously not null, it will go to the left node and the right node of it as well (we will come to this in a second).

Now when it will come to 4, both of it has NULL as its children, a.k.a 0, so it returns MAX(0,0) + 1, which is 1. Following this, 2 has recieved a value of 1 from its left side, and its right side is NULL, so it returns MAX(0, 1) + 1, which is 2.

So now, 6 has recieved a value of 2 from its left sub-branch. If we follow this pattern on the right as well, it will also receive a value of 2 from the right. The final height of the tree would be MAX(2,2), which is equal to 3. Hence we arrive at our final answer.

It should not be TOO hard to create code for the minimum depth, so it is a challenge for you to figure out on your own. But here is the code regardless.

int minDepth(struct TreeNode* root) {
  if (root == NULL) {
    return 0;
  }
  if (root->left == NULL && root->right == NULL)
    return 1;
 
  int left = INT_MAX;
  int right = INT_MAX;
 
  if (root->left != NULL) {
  left = minDepth(root->left);
  }
 
  if (root->right != NULL) {
  right = minDepth(root->right);
  }
 
  if (left < right) {
    return left + 1;
  } else {
    return right + 1;
  }
}

INT_MAX is used as a placeholder for an invalid or non-existent value when computing the minimum depth of a binary tree. INT_MAX represents the largest possible integer value (essentially infinity in this case) to ensure that non-existent child nodes do not affect the minimum calculation.

Width / Diameter of a binary tree.

Width / Diameter of a binary tree is the farthest distance between any two nodes.

int height(struct TreeNode* root) {
  if (root == NULL) {
    return 0;
  }
 
  int left = height(root->left);
  int right = height(root->right);
 
  if (left > right) {
    return left + 1;
  } else {
    return right + 1;
  }
}
 
int diameterOfBinaryTree(struct TreeNode* root) {
  if (root == NULL) {
    return 0;
  }
 
  int a = diameterOfBinaryTree(root->left);
  int b = diameterOfBinaryTree(root->right);
  int c = height(root->left) + height(root->right);
 
  if (a > b && a > c)
      return a;
  if (b > a && b > c)
      return b;
  if (c > a && c > b)
      return c;
}

Well, when we search for the diameter, its not necessary that it will span from the left subtree to the root to the right subtree. There are 3 ways to get the diameter:

1. You start from left subtree and end in the left subtree, which is why we call diameterOfBinaryTree(root->left).
2. You start from the right subtree and end in the right subtree, which is why we call diameterOfBinaryTree(root->right).
3. You start from the left subtree and end in the right subtree, which is why we call height(root->left) + height(root->right).

But a problem with this bruteforced technique is that we have another recursive call inside a recursive call, which essentially makes our time complexity O(n^2). So we need some way to not call the height function. Let us create a new function and a new struct outside our main diameterOfBinaryTree function.

struct Pair {
  int first;
  int second;
};
 
struct Pair diameterFast(struct TreeNode* root) {
  if (root == NULL) {
    struct Pair p = {0, 0};
    return p;
  }
 
  struct Pair left = diameterFast(root->left);
  struct Pair right = diameterFast(root->right);
 
  int a = left.first;
  int b = right.first;
  int c = left.second + right.second;
 
  struct Pair pair;
 
  if (a > b && a > c) {
    pair.first = a;
  } else if (b > a && b > c) {
    pair.first = b;
  } else if (c > a && c > b) {
    pair.first = c;
  }
 
  if  (left.second > right.second) {
    pair.second = left.second + 1;
  } else {
    pair.second = right.second + 1;
  }
 
  return pair;
}

And now using this function, in our main function.

int diameterOfBinaryTree(struct TreeNode* root) {
  return diameterFast(root).first;
}

If it not obvious, in the Pair struct, we save second as the height of the trees as we go along the tree, so we need not make another height function to calculate it.

Checking for balanced trees

A definition for a balanced tree is that if the difference between heights of left and eight subtree is not more than one for all nodes of the tree.

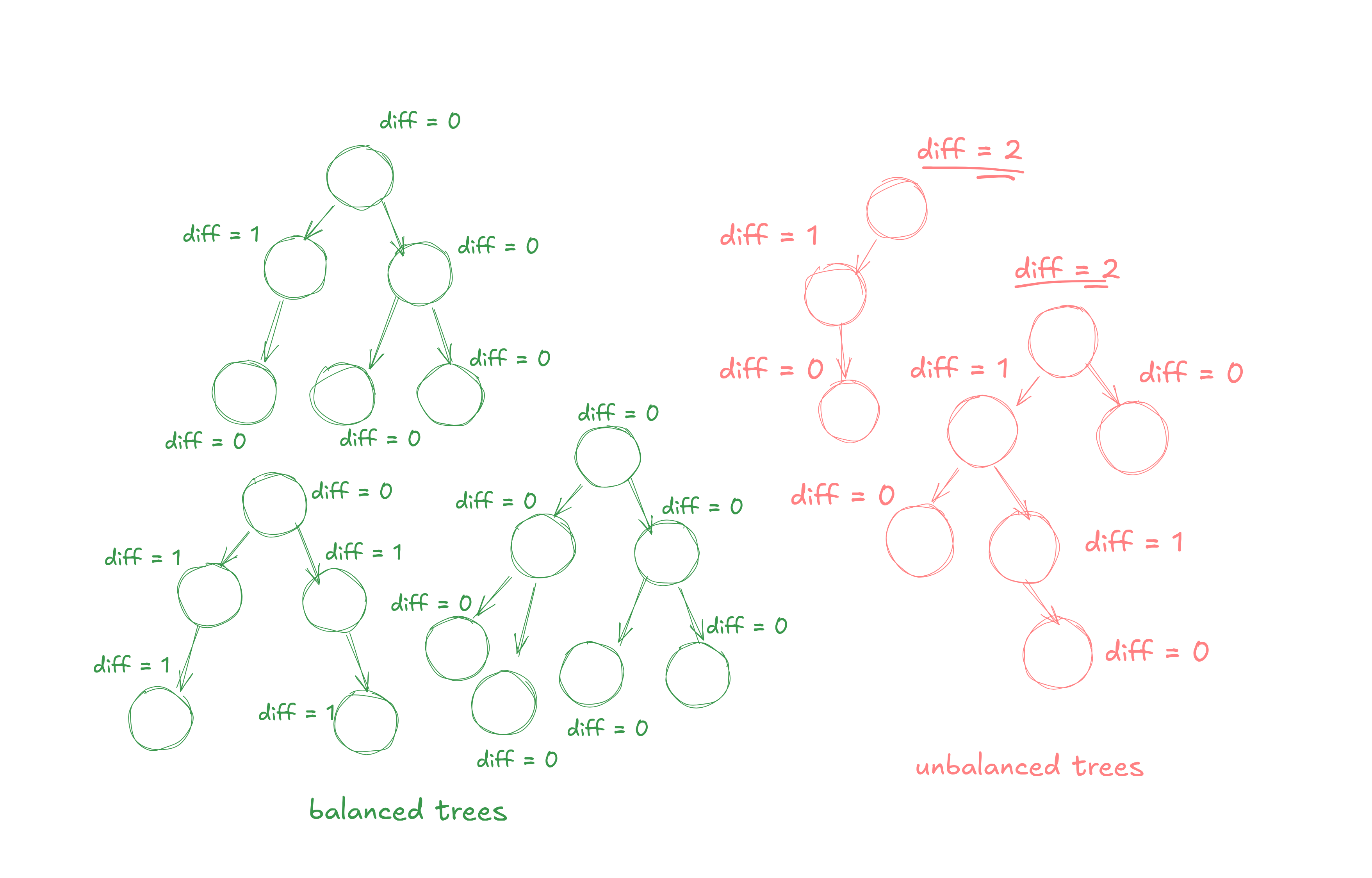
So to basically speak, we can create this formula

and looking up to our previous code, we know how to find the height. so simply coding it we get

int isBalanced(struct TreeNode *root) {
  if (root == NULL) {
    return 1;
  }
 
  int left = isBalanced(root->left);
  int right = isBalanced(root->right);
 
  int diff = abs(height(root->left) - height(root->right));
 
  if (left && right && diff) {
    return 1;
  } else {
    return 0;
  }
}

But with this solution, we arrive at the same dilemma, the time complexity being O(n^2). We need to track the height while travesing.

struct Pair isBalancedFast(struct TreeNode* root) {
  if (root == NULL) {
    struct Pair p = {0, 0};
    return p;
  }
 
  struct Pair left = isBalancedFast(root->left);
  struct Pair right = isBalancedFast(root->right);
 
  int a = left.first;
  int b = right.first;
  int c = abs(left.second + right.second) <= 1;
 
  struct Pair pair;
 
  if (a && b && c) {
    pair.first = 1;
  } else {
    pair.first = 0;
  }
 
  if  (left.second > right.second) {
    pair.second = left.second + 1;
  } else {
    pair.second = right.second + 1;
  }
 
  return pair;
}

and then using this function in our main function, we get

int isBalanced(struct TreeNode *root) {
  return isBalancedFast(root).first;
}

Zig Zag Traversal

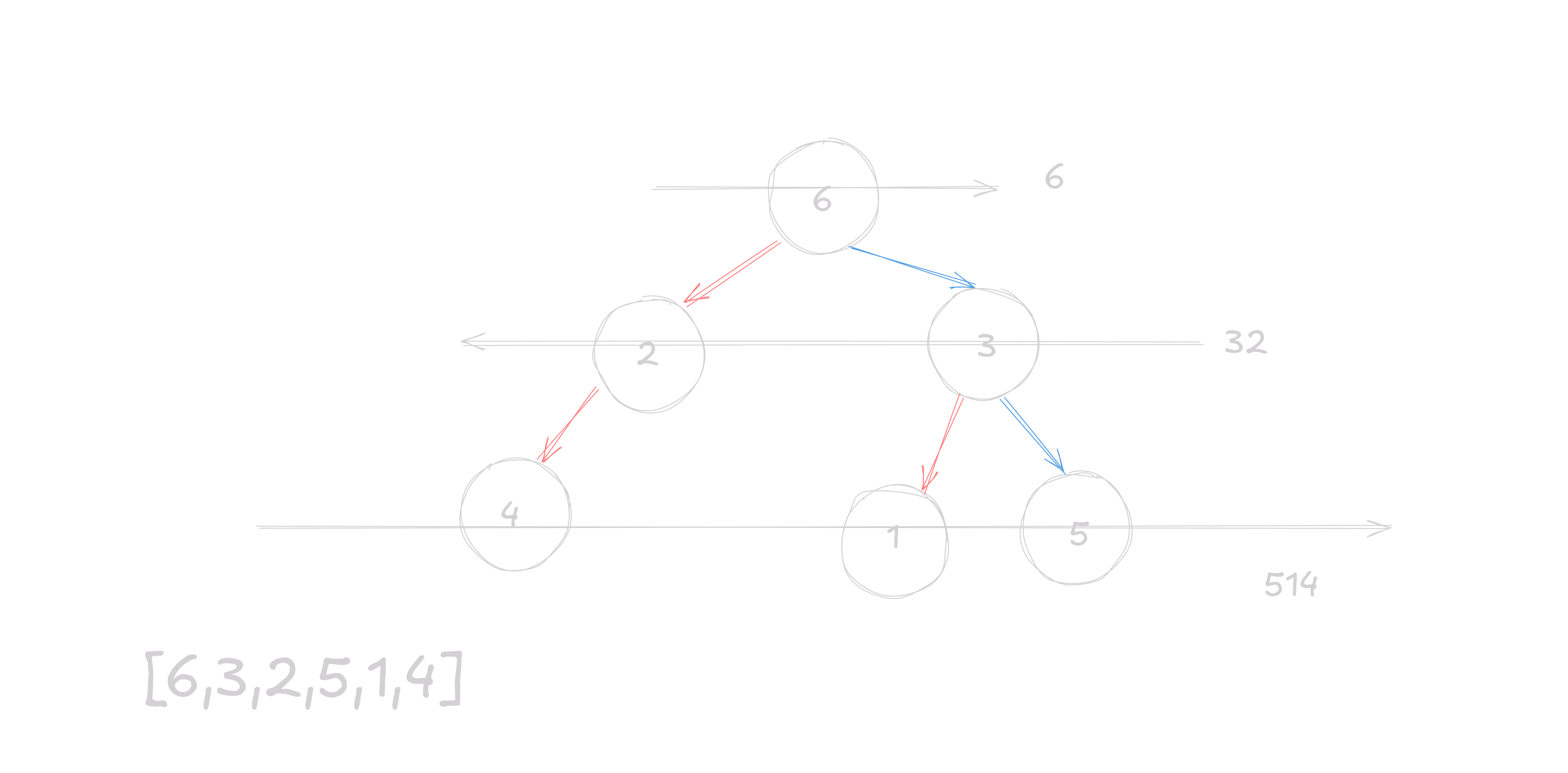
Zig Zag traversal is pretty easy to understand, we go once left to right then on next layer right to left, and then we alternate between these until we reach the end of the tree.