Recursion

Recursion might be one of the most important concepts in the field of DSA. Without that, you cannot do graphs, trees, backtracking, divide and conquer, etc. At first, it feels useless, it feels as if using loops is better. But as you progress, you will see that recursion is a very powerful tool.

You need to know about the following topics before starting this

1. Functions
2. Memory Management

Let us start with this code

void print_three() {
    printf("3\n");
}
 
void print_two() {
    printf("2\n");
    print_three();
}
 
void print_one() {
    printf("1\n");
    print_two();
}
 
int main() {
    print_one();
    return 0;
}

Well, this will obviously print 1 2 3. But from previous notes, we know that each function makes a stack frame and it will be their as long as the function is running. So, when print_one calls print_two, the stack frame of print_one is still there, same with print_two when it calls print_three. But this code is obviously bad, so us use recursion to make it better.

void print(int n) {
    printf("%d\n", n);
    print(n + 1);
}
 
int main() {
    print(1);
    return 0;
}

Effective, what now happens in that when print is called, it will print the number and then create another stackframe for itself but with the argument n + 1. But this program does not know when to stop printing, hence it will print numbers infinitely. This is called infinite recursion.

We need to have an condition to stop the recursion. This is called the base case. Let us modify the code to have a base case.

void print(int n) {
    if (n > 3) {
        return;
    }
    printf("%d\n", n);
    print(n + 1);
}
 
int main() {
    print(1);
    return 0;
}

Now this code checks if the number is greater than or equal to 3, if it is, it will return and the recursion will stop. Now, this will print

1
2
3

Well these were the basics of recursion.

Factorial

The factorial of a number is the product of all positive integers less than or equal to that number. The factorial of 0 is 1. Mathematically

The base case here would be that n is less than or equal to 1, in which case we return 1.

int factorial(int n) {
    if (n <= 1) {
        return 1;
    }
    return n * factorial(n - 1);
}

Fibonacci Series

The Fibonacci Series is a series of numbers in which each number is the sum of the two preceding ones, usually starting with 0 and 1. Let us write a function to get the nth Fibonacci number.

The basic idea is that

Visualizing F(2), we get

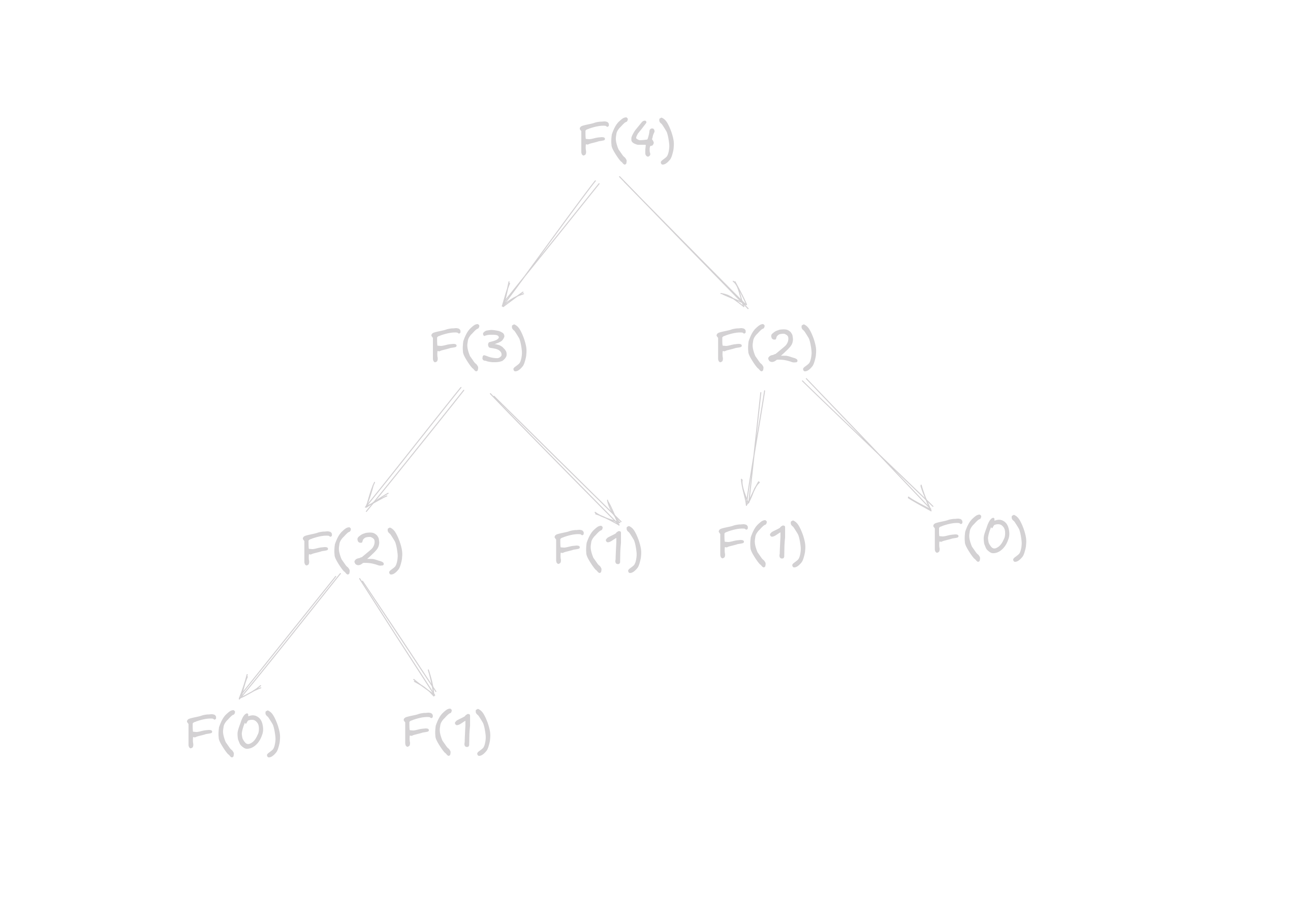
The base case for this is that if n is less than or equal to 1, we return n.

int fibo(int n) {
    if (n <= 1) {
        return n;
    }
    return fibo(n - 1) + fibo(n - 2);
}

This is almost all you need to know about recursion, and this will come in handy in a LOT of structures and algorithms.