The Big O Notation

source

Time and Space Complexity

big-0

The later parts of this document will contain some high school level mathematics. If you are not comfortable with that, I would highly recommend you to go through the chapter "Relations and Functions".

Need For Big O and Time Complexity

Suppose these two codes written in python. Their task is to find the letter i in the word inputted by the user.

word = input()
if i in word:
    print("Found i")

The second code

word = input()
for letter in word:
    if letter == 'i':
        print("Found i")

Now if we were to run the first code on a piece of junk, and second one on a supercomputer, the supercomputer might execute it faster, but in the terms of Big O, the first code is faster. This is because the first code has a time complexity of O(1) and the second code has a time complexity of O(n).

So, Time Complexity is a way to represent how much time an algorithm takes to run, in terms of the input size. How do we see it mathematically? Well we can plot a graph of the time taken by the algorithm to run, against the input size. This graph is called the Time Complexity Graph. So let us take some example code.

int main() {
    for (int i = 0; i < n; i++) {
        printf("Hello, World!");
    }
}

Here we can see that n and time are directly proportional. Therefore the graph would look something like this. Theta in the graph is called the rate of increase of time taken by the algorithm. And this rate is referred to as the Time Complexity of the algorithm.

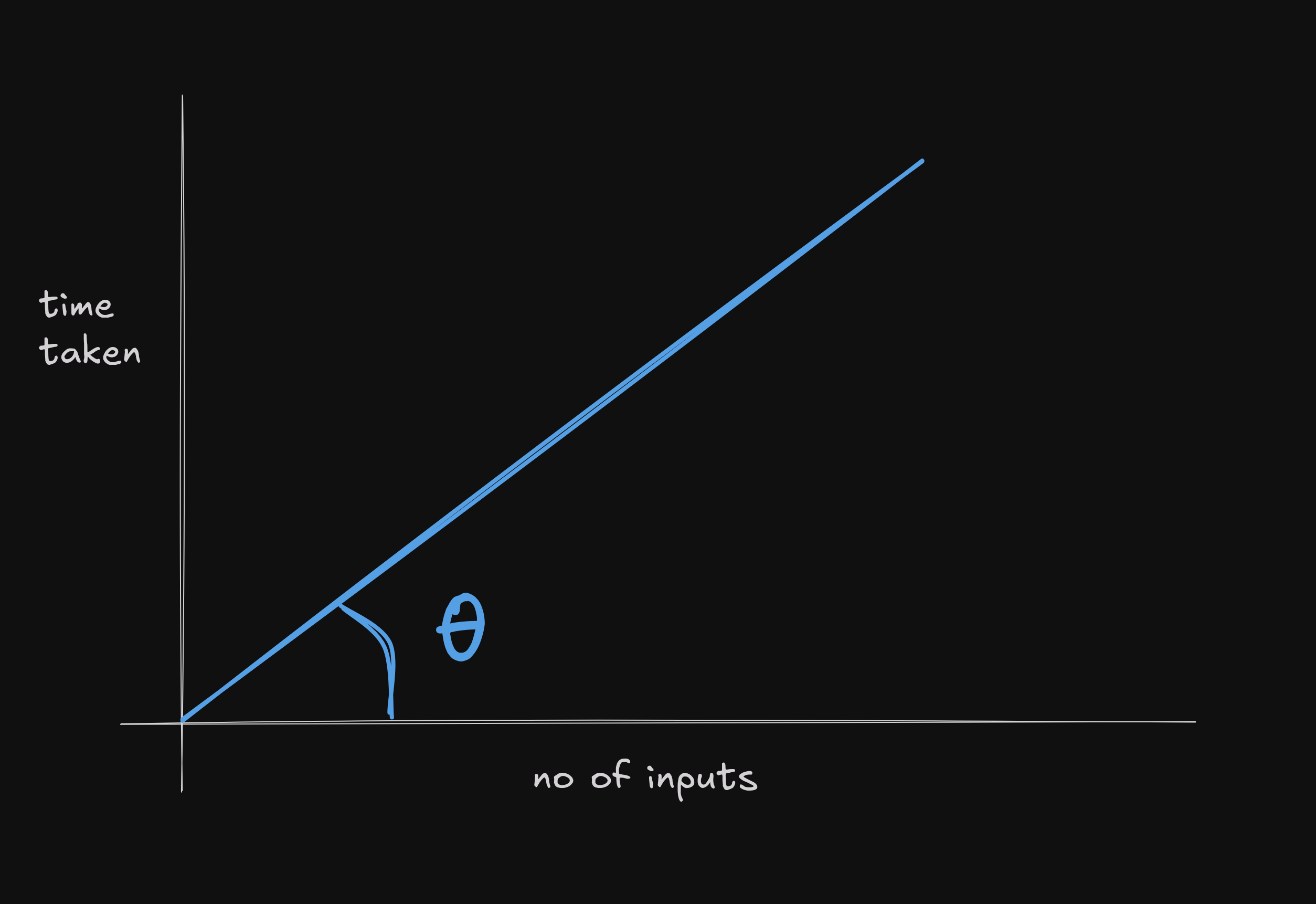
Similarly space complexity is a way to represent how much space an algorithm takes to run, in terms of the input size. It is also represented in terms of the input size.

Big O Notation

Big O Notation is a way to represent the time complexity of an algorithm. It is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. It is used to describe the upper bound of the time complexity of an algorithm. It's like saying, "The time complexity of this algorithm will never be more than this." We write as O(x), where x is the term of time complexity with the highest degree (without the coeffecient) of the algorithm. You just need to remember 3 rules while calculating the Big O of an algorithm.

Always consider the worst case scenario.
Ignore the constants.
Ignore the lower terms.

Analyzing Algorithms

Let's take an example of a simple algorithm to swap two variables.

void swap(int a, int b) {
    int temp = a;
    a = b;
    b = temp;
}

We will assume that each statement in the code takes 1 unit of time to execute. So the time function would be T(n) = 1 + 1 + 1 = 3. For the space complexity, we have a, b, and the temp variable, therefore the space function would be S(n) = 1 + 1 + 1 = 3. In terms of Big O, the time complexity would be O(1) and the space complexity would also be O(1).

Frequncy Count Method

This method is used to calculate the time complexity of an algorithm. It is done by counting the number of times a statement is executed. Let's take an example of a simple algorithm to find the sum of the first n natural numbers.

int main() {
  sum = 0;
  n = 10;
  for (int i = 1; i <= n; i++) {
    sum += i;
  }
}

Here the for loop is actually made of three smaller statements. The initialization of i, the condition, and then finally, the increment. The initialization would only be executed once. The condition i <= n would be checked for a n+1 times (because it is <=) and then finally the increment will happen n times.

Therefore, the time complexity of this algorithm would be T(n) = 1 + 1 + 1 + n + n = 2n + 3 (the beginning 2 ones are for initializing sum and n). In terms of Big O, the time complexity would be O(n).

For the space complexity, we have sum, n, and i, therefore the space function would be S(n) = 1 + 1 + 1 = 3. In terms of Big O, the space complexity would be O(1).

Let us take another example of adding two matrices, where the size is given as n x n.

void add(int *A, int *B, int *C, int n) {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            C[i * n + j] = A[i * n + j] + B[i * n + j];
        }
    }
}

Now we know that the first for loop would run for n times, the second nested for loop would run for n * (n + 1) times and each line in the second nested loop would run for n * n times. Therefore the time complexity turns out to be T(n) = n^2 + n + n^2 = 2n^2 + n

For the space complexity, we have A, B, C and i,j,n.

A, B and C are 2 dimensional arrays, therefore they would take n * n space. And i, j, n would take 1 space. Therefore the space complexity would be S(n) = 3n^2 + 3. In terms of Big O, the time complexity would be O(n^2) and the space complexity would also be O(n^2).

Some Rapid Fire Examples

void fun(int n) {
    for (int i = 0; i < n; i+=2) {
        printf("%d", i);
    }
}

So what if instead of 1 step increment, it was two steps like shown above? Well the for loop would run for n/2 times. Therefore the time complexity would be O(n/2). But we ignore the constants, therefore the time complexity would be O(n).

The space complexity would be S(n) = 2, so the space complexity would be O(1).

void fun(int n) {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < i; j++) {
            printf("%d", i + j);
        }
    }
}

The above code is just a classic double nested loop but instead of j running for n times, it runs for i times. If it confuses you let me illustrate it.

So this code as well will have the time complexity of O(n^2). Space complexity would be O(1).

for (int i = 1; i < n; i*=2) {
    printf("%d", i);
}

Calculating the time complexity of this code is kind of interesting. So after the code has run, the value of i would be greater than n. And we also know that the value of I would be a power of 2, let it be 2^k So after the loop, we can say that

$i >= n$

$i = 2^k$

$2^k >= n$

$k >= log_2(n)$

The time complexity would be O(log(n)). The space complexity would be O(1). Let us solve another problem this way

for (int i = 1; i*i < n; i++) {
    printf("%d", i);
}

After the loop has run, the value of i^2 will be greater than n

$i^2 >= n$

$i >= \sqrt{n}$

Therefore the time complexity would be O(sqrt(n)). The space complexity would be O(1).

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j*=2) {
        printf("Hello");
    }
}

The inner loop will have a time complexity of O(log(n)) and the outer loop will have a time complexity of O(n). The time complexity of the code now becomes O(n * log(n)). The space complexity would be O(1).

Analysis of IF and WHILE

Time analysis of while loops are similar to that of for loops. Let us examine a while loop

int i = 0;
while (i < n) {
    printf("%d", i);
    i++;
}

Like the for loop, the condition check would run for n+1 times, all the lines in the for loop would run for n times, and there is an initialization statement of i which will take 1 unit of time. Therefore the time complexity would be T(n) = 1 + n + 1 + n + n = 3n + 2 or O(n). The space complexity would be O(1).

If conditions only divide the execution of code into two parts, which can give varying time complexities for different inputs.

if (n % 2 == 0) {
    printf("Even");
} else {
    for (int i = 0; i < n; i++) {
        printf("%d", i);
    }
}

So in this case, if the input is even, the time complexity would be O(1), but if the input is odd, the time complexity would be O(n). So O(1) is the best case time complexity and O(n) is the worst case time complexity.

Common Time Complexities

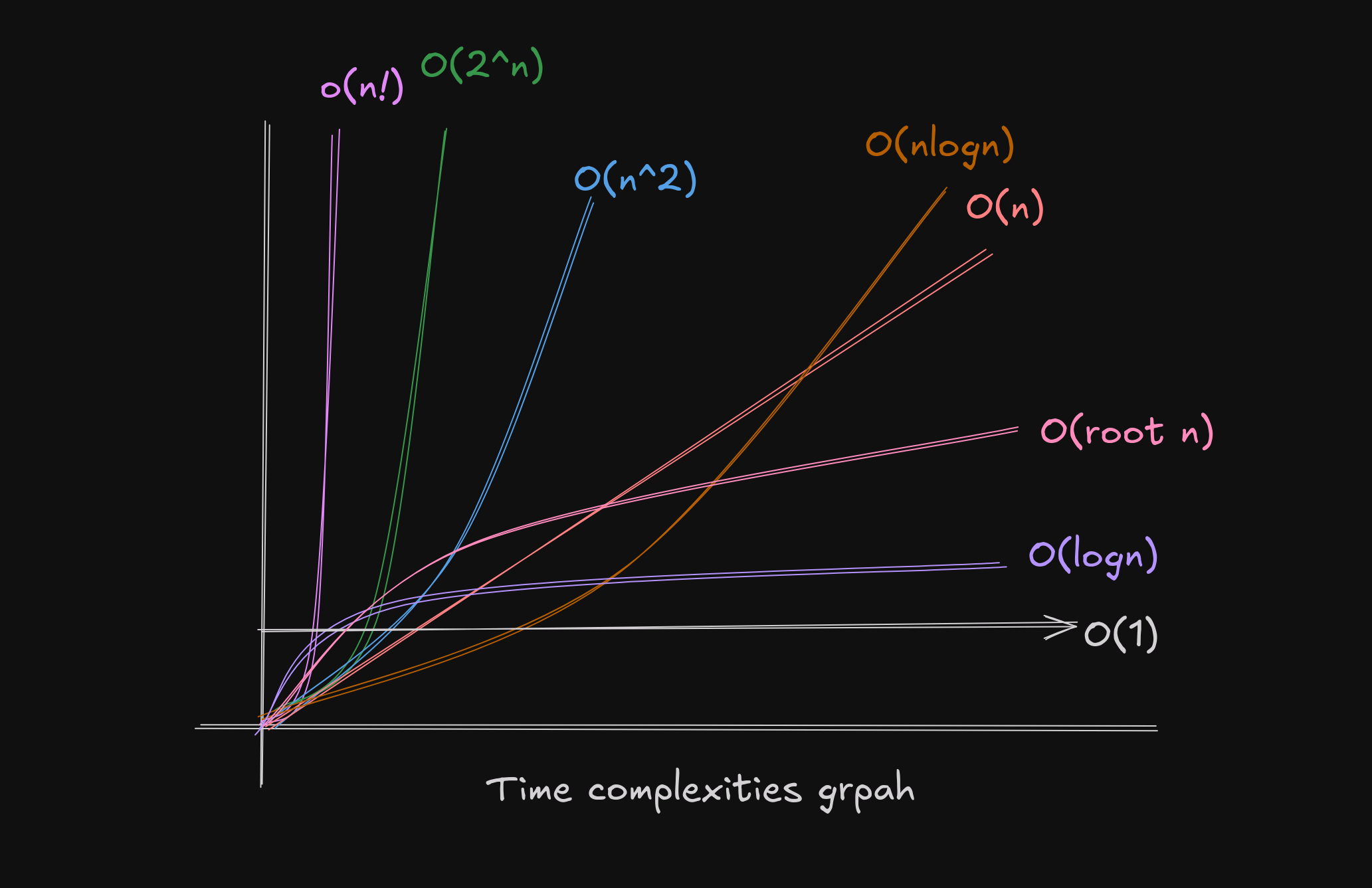
During solving questions, here are some common time complexities that you will encounter. Here are them in order of increasing time complexity.

$O(1) < O(log(n)) < O(\sqrt{n}) < O(n) < O(nlog(n)) < O(n^2) < O(2^n) < O(n!)$

Here is a rough graph of the time complexities

Asymptotic Notations

Here is the mathematical definition of Big Oh:

$f(n) = O(g(n)) \iff \exists c > 0, n_0 > 0 : \forall n \geq n_0, |f(n)| \leq c|g(n)|$

In human readable english: it would be defined as -

A function f(n) is said to be Big O of g(n), written as f(n) = O(g(n)), if and only if there exist positive constants c and n₀ such that for all values of n greater than or equal to n₀, the absolute value of f(n) is less than or equal to c times the absolute value of g(n).

Let us suppose we write the inquality

$2n + 2 <= 8n$

This inequality is true for all values of n greater than or equal to 1. Here we can see that $2n + 2 = O(n)$ is $f(n)$ , and $n$ is $g(n)$ . The constants $c$ is 8. Therefore,

$f(n) = O(n)$

Now, recalling the series from earlier

$O(1) < O(log(n)) < O(\sqrt{n}) < O(n) < O(nlog(n)) < O(n^2) < O(2^n) < O(n!)$

O(n) is the average bound when f(n) = 2n + 2, all the Os on the right of it become the upper bound and all of them on the left, become the lower boud.

Now here is the mathematical definition of Big Omega:

$f(n) = \Omega(g(n)) \iff \exists c > 0, n_0 > 0 : \forall n \geq n_0, f(n) \geq c \cdot g(n)$

The only difference between Big Oh and Big Omega is the reverse inequality sign. Big Omega is used to define the lower bound of a function. and there is also the theta notation.

And then there is also the big theta notation

$f(n) = \Theta(g(n)) \iff \exists c_1, c_2 > 0, n_0 > 0 : \forall n \geq n_0, c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)$

or in mathematical terms:

A function f(n) is said to be Big Theta of g(n), written as f(n) = Θ(g(n)), if and only if there exist positive constants c₁, c₂, and n₀ such that for all values of n greater than or equal to n₀, c₁ times g(n) is less than or equal to f(n), which in turn is less than or equal to c₂ times g(n).

Big Theta notation provides both an upper and lower bound on the growth rate of a function. It's used when a function grows at exactly the same rate as another function, up to constant factors. In algorithm analysis, Big Theta gives the exact order of growth for an algorithm's time or space complexity.

Let us take some polynomial functions to understand the concept of aympotic notations.

$f(n) = 2n^2 + 3n + 4$

Now for all positive integers values of n,

$2n^2 + 3n + 4 <= 2n^2 + 3n \times n + 4 \times n^2$

and this could further be simplified to

$2n^2 + 3n + 4 <= 9n^2$

Now $g()$ becomes $n^2$ and $c$ becomes 9.

Therefore, $f(n) = O(n^2)$ This is the Big-Oh.

Now for the same function, I can also say:

$2n^2 + 3n + 4 >= 1 \times n^2$

and also:

$1 \times n^2 <= 2n^2 + 3n + 4 <= 9n^2$

So the big omega would be $f(n) = \Omega(n^2)$ and big theta would also be $f(n) = \Theta(n^2)$

Properties of Asymptotic Notations

If we multiply a function by a constant, the time complexity remains the same.
Transitive property: If $f(n) = O(g(n))$ and $g(n) = O(h(n))$ , then $f(n) = O(h(n))$
Reflexive property: $f(n) = O(f(n))$
Symmetric property: If $f(n) = \Theta(g(n))$ , then $g(n) = \Theta(f(n))$ . This property is only valid for Big Theta.
Transpose Symmetric property: If $f(n) = O(g(n))$ , then $g(n) = \Omega(f(n))$ .

And this concludes the Big O notation and the asymptotic notations. I hope you have a better understanding of the time complexities and the asymptotic notations. If you have any questions, always feel free to ask me on x.

my web

x dot com